An Overview of R

# An Overview of R - 2

## Introductory Computer Programming

### Deepayan Sarkar

---

# Before we start, an experiment!

Color combination: Is it __white & gold__  or __blue & black__ ? Let's count!

```r
NN <- 18 + 8 # total
XX <- 18     # white and gold
```

---

# Question: What proportion of population sees white & gold?

- Statistics uses data to make inferences

- Model:

- Let $p$ be the probability of seeing white & gold

- Assume that individuals are independent
--

- Data:

- Suppose $X$ out of $N$ sampled individuals see white & gold; 
	  e.g., $N = 26$, $X = 18$.

- According to model, $X \sim Bin(N, p)$
--

- "Obvious" estimate of $p = X / N = 18 / 26 = 0.6923$

- But how is this estimate derived?

---

# Generally useful method: maximum likelihood

- Likelihood function: probability of observed data as function of $p$

$$
L(p) = P(X = 18) = {26 \choose 18}  p^{18} (1-p)^{(26-18)}, p \in (0, 1)
$$

- Intuition: $p$ that gives higher $L(p)$ is more "likely" to be correct

- Maximum likelihood estimate $\hat{p} = \arg \max L(p)$
--

- By differentiating 
$$
\log L(p) = c + 18 \log p + 8 \log (1-p)
$$
we get
$$
\frac{d}{dp} \log L(p) = \frac{18}{p} - \frac{8}{1-p} = 0 \implies 18 (1-p) - 8 p = 0 \implies p = \frac{18}{26}
$$

---

# How could we do this numerically?

- Pretend for the moment that we did not know how to do this.

- How could we arrive at the same solution numerically?

- Basic idea: Compute $L(p)$ for various values of $p$ and find minimum.
--

- To do this in R, remember that R works like a calculator:

- The user types in an expression, R calculates the answer

- The expression can involve numbers, variables, and functions

- For example:

```r
N = NN
x = XX
p = 0.5
choose(N, x) * p^x * (1-p)^(N-x)
```

```
[1] 0.02327971
```

---

# "Vectorized" computations

- One important distinguishing feature of R is that it operates on "vectors"

```r
pvec = seq(0, 1, by = 0.01)
pvec
```

```
  [1] 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18
 [20] 0.19 0.20 0.21 0.22 0.23 0.24 0.25 0.26 0.27 0.28 0.29 0.30 0.31 0.32 0.33 0.34 0.35 0.36 0.37
 [39] 0.38 0.39 0.40 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49 0.50 0.51 0.52 0.53 0.54 0.55 0.56
 [58] 0.57 0.58 0.59 0.60 0.61 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.70 0.71 0.72 0.73 0.74 0.75
 [77] 0.76 0.77 0.78 0.79 0.80 0.81 0.82 0.83 0.84 0.85 0.86 0.87 0.88 0.89 0.90 0.91 0.92 0.93 0.94
 [96] 0.95 0.96 0.97 0.98 0.99 1.00
```

```r
Lvec = choose(N, x) * pvec^x * (1-pvec)^(N-x)
Lvec
```

```
  [1] 0.000000e+00 1.441581e-30 3.484224e-25 4.743664e-22 7.744746e-20 3.953724e-18 9.671700e-17
  [8] 1.423593e-15 1.444375e-14 1.102691e-13 6.725082e-13 3.419368e-12 1.495827e-11 5.766228e-11
 [15] 1.995491e-10 6.291462e-10 1.828738e-09 4.948377e-09 1.256532e-08 3.014411e-08 6.870958e-08
 [22] 1.495277e-07 3.119770e-07 6.263028e-07 1.213580e-06 2.275976e-06 4.141251e-06 7.326358e-06
 [29] 1.262589e-05 2.123187e-05 3.489188e-05 5.611264e-05 8.841550e-05 1.366491e-04 2.073621e-04
 [36] 3.092354e-04 4.535679e-04 6.548064e-04 9.310987e-04 1.304845e-03 1.803214e-03 2.458572e-03
 [43] 3.308786e-03 4.397325e-03 5.773111e-03 7.490042e-03 9.606132e-03 1.218220e-02 1.528011e-02
 [50] 1.896044e-02 2.327971e-02 2.828716e-02 3.402104e-02 4.050475e-02 4.774279e-02 5.571678e-02
 [57] 6.438184e-02 7.366353e-02 8.345564e-02 9.361912e-02 1.039824e-01 1.143435e-01 1.244734e-01
 [64] 1.341224e-01 1.430267e-01 1.509184e-01 1.575359e-01 1.626355e-01 1.660037e-01 1.674691e-01
 [71] 1.669138e-01 1.642827e-01 1.595904e-01 1.529252e-01 1.444492e-01 1.343941e-01 1.230530e-01
 [78] 1.107677e-01 9.791332e-02 8.487885e-02 7.204722e-02 5.977459e-02 4.837120e-02 3.808505e-02
 [85] 2.909005e-02 2.147970e-02 1.526701e-02 1.039084e-02 6.728148e-03 4.110731e-03 2.344891e-03
 [92] 1.231523e-03 5.843301e-04 2.439130e-04 8.615269e-05 2.424055e-05 4.910431e-06 5.924050e-07
 [99] 2.780141e-08 1.303740e-10 0.000000e+00
```

---

# Plotting is very easy

```r
plot(x = pvec, y = Lvec, type = "l")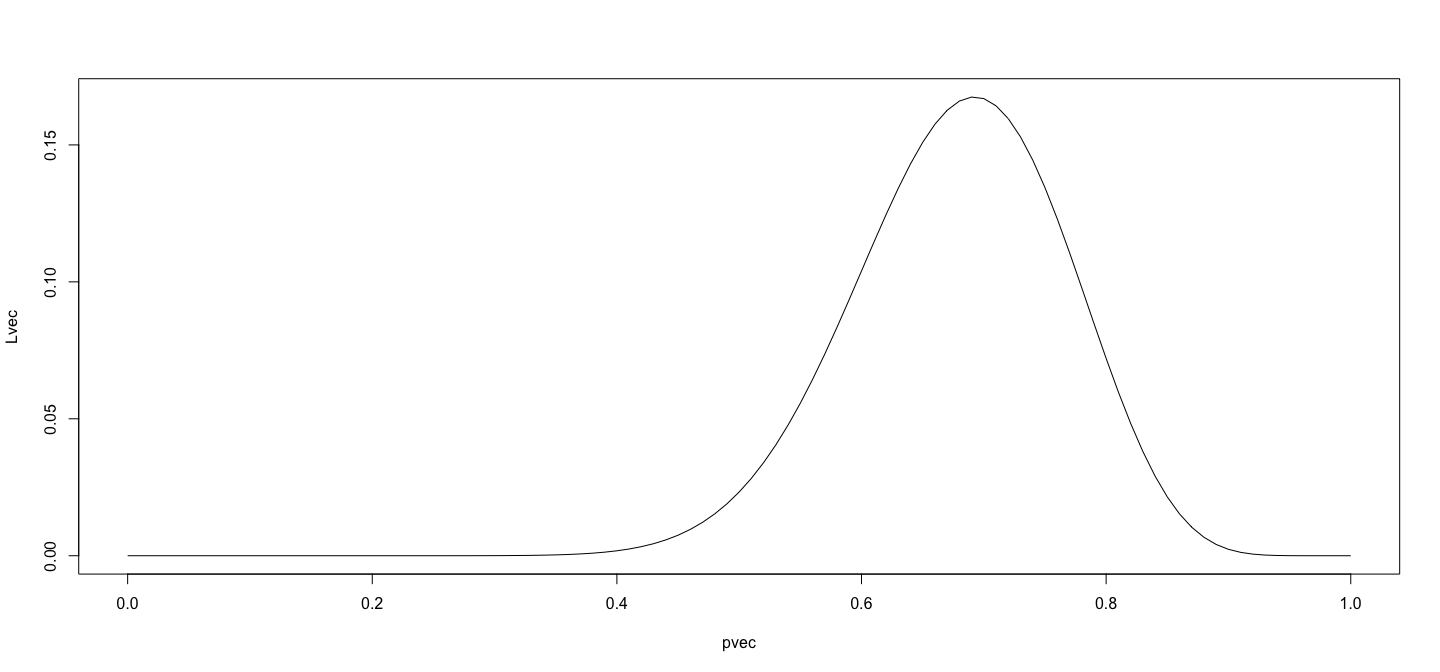
```

![plot of chunk unnamed-chunk-4](figures/roverview-2-unnamed-chunk-4-1.png)

---

# Functions

- Functions can be used to encapsulate repetitive computations

- Like mathematical functions, they take arguments as input and "returns" an output

```r
L = function(p) choose(N, x) * p^x * (1-p)^(N-x)
L(0.5)
```

```
[1] 0.02327971
```

```r
L(x/N)
```

```
[1] 0.1675234
```

---

# Functions can be plotted directly

```r
plot(L, from = 0, to = 1)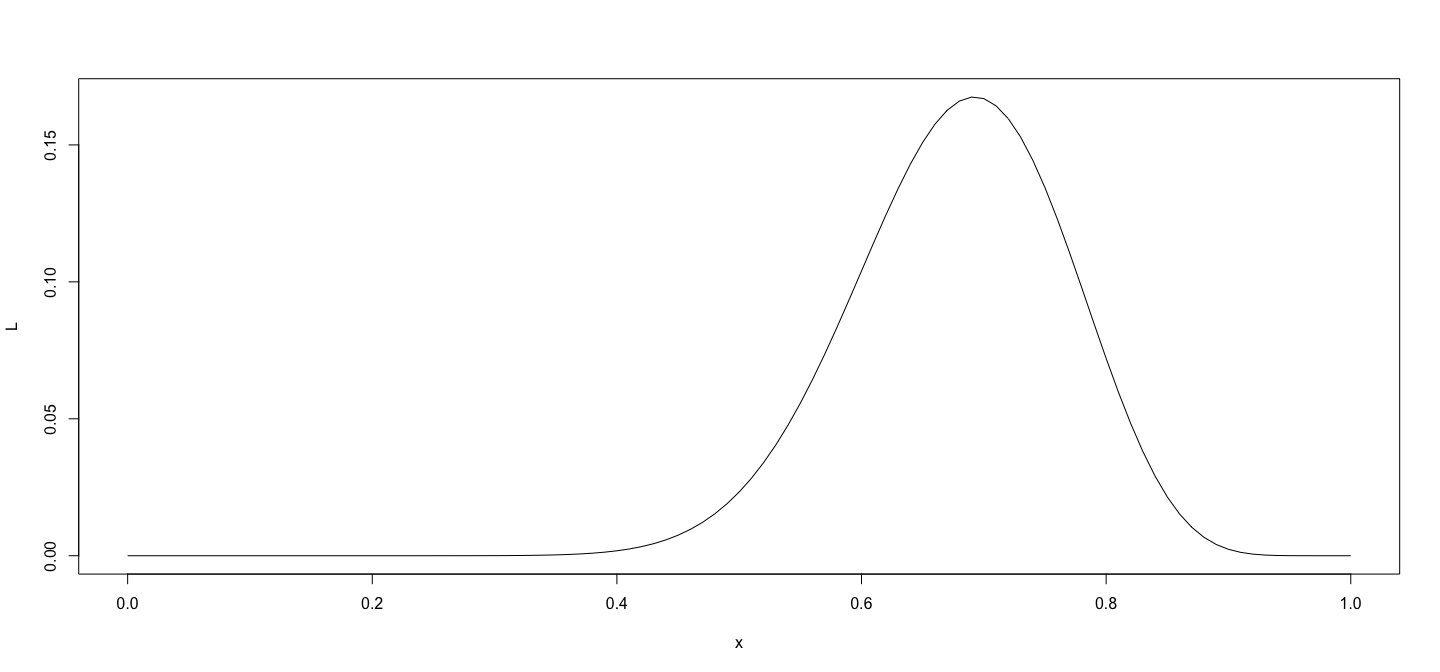
```

![plot of chunk unnamed-chunk-6](figures/roverview-2-unnamed-chunk-6-1.png)

---

# ...and they can be numerically "optimized"

```r
optimize(L, interval = c(0, 1), maximum = TRUE)
```

```
$maximum
[1] 0.6923109

$objective
[1] 0.1675234
```

- Compare with

```r
XX / NN
```

```
[1] 0.6923077
```

---

# Another example: Linear regression

```r
data(Davis, package = "carData")        # Davis height and weight data
str(Davis)                              # Summarize structure of data
```

```
'data.frame':	200 obs. of  5 variables:
 $ sex   : Factor w/ 2 levels "F","M": 2 1 1 2 1 2 2 2 2 2 ...
 $ weight: int  77 58 53 68 59 76 76 69 71 65 ...
 $ height: int  182 161 161 177 157 170 167 186 178 171 ...
 $ repwt : int  77 51 54 70 59 76 77 73 71 64 ...
 $ repht : int  180 159 158 175 155 165 165 180 175 170 ...
```

```r
fm <- lm(weight ~ height, data = Davis) # Regression of weight on height
fm
```

```

Call:
lm(formula = weight ~ height, data = Davis)

Coefficients:
(Intercept)       height  
    25.2662       0.2384  
```

---

# You should always plot the data first!

```r
library(lattice) # A different way to plot data
xyplot(weight ~ height, data = Davis, grid = TRUE, type = c("p", "r"))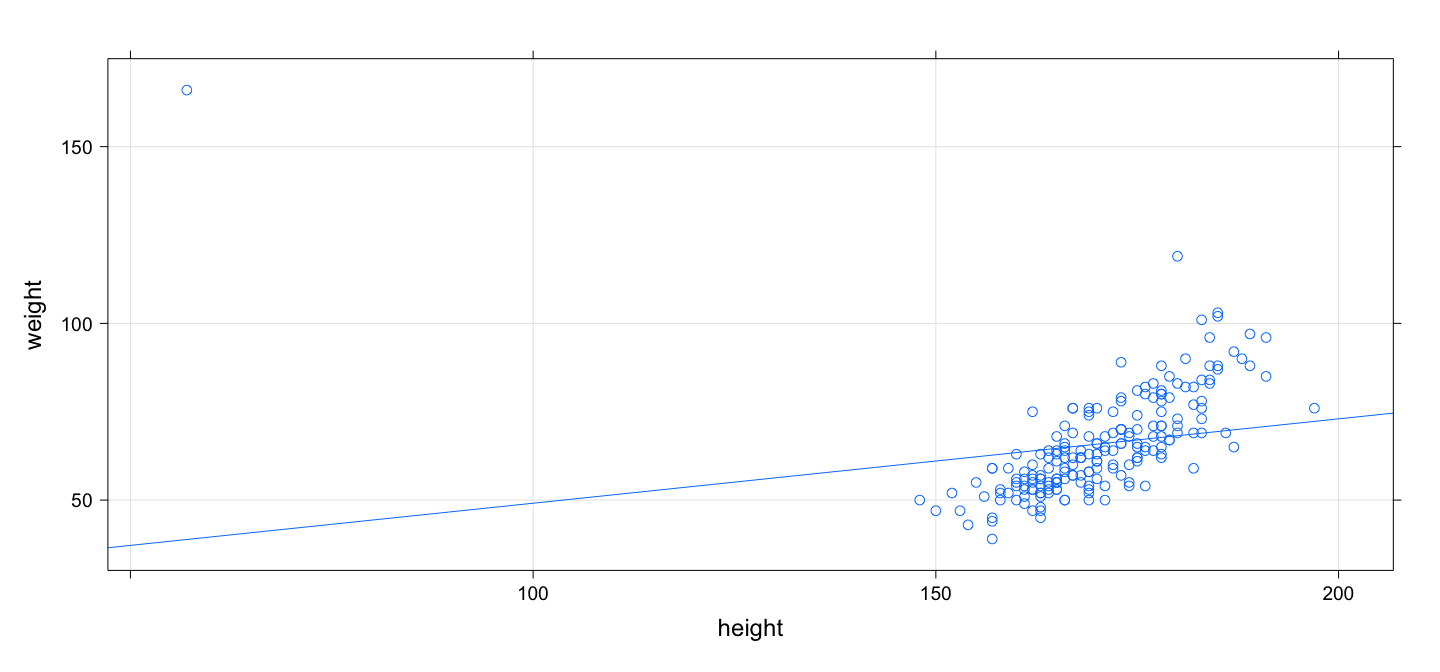
```

![plot of chunk unnamed-chunk-10](figures/roverview-2-unnamed-chunk-10-1.png)

---

# The regression model is fit by minimizing least squares

```r
coef(fm) # estimated regression coefficients
```

```
(Intercept)      height 
 25.2662278   0.2384059 
```
--

- We can confirm using a general optimizer:

```r
SSE = function(beta)
{
    with(Davis,
         sum((weight - beta[1] - beta[2] * height)^2))
}
optim(c(0, 0), fn = SSE)
```

```
$par
[1] 25.3053648  0.2381936

$value
[1] 43713.12

$counts
function gradient 
      99       NA

$convergence
[1] 0

$message
NULL
```

---

# Fitting the regression model

- `lm()` gives exact solution and more statistically relevant details

```r
summary(fm)
```

```

Call:
lm(formula = weight ~ height, data = Davis)

Residuals:
    Min      1Q  Median      3Q     Max 
-23.696  -9.506  -2.818   6.372 127.145

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) 25.26623   14.95042   1.690  0.09260 . 
height       0.23841    0.08772   2.718  0.00715 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 14.86 on 198 degrees of freedom
Multiple R-squared:  0.03597,	Adjusted R-squared:  0.0311 
F-statistic: 7.387 on 1 and 198 DF,  p-value: 0.007152
```

---

# Changing the model-fitting criteria

- Suppose we wanted to minimize _sum of absolute errors_ instead of sum of squares

- No closed form solution any more, but general optimizer will still work:

```r
SAE = function(beta)
{
    with(Davis,
         sum(abs(weight - beta[1] - beta[2] * height)))
}
opt = optim(c(0, 0), fn = SAE)
opt
```

```
$par
[1] -106.000787    1.000005

$value
[1] 1504

$counts
function gradient 
     169       NA

$convergence
[1] 0

$message
NULL
```

---

# This is an example of _robust regression_

```r
xyplot(weight ~ height, data = Davis, grid = TRUE,
       panel = function(x, y, ...) {
           panel.abline(fm, col = "red") # squared errors
           panel.abline(opt$par, col = "blue") # absolute errors
           panel.xyplot(x, y, ...)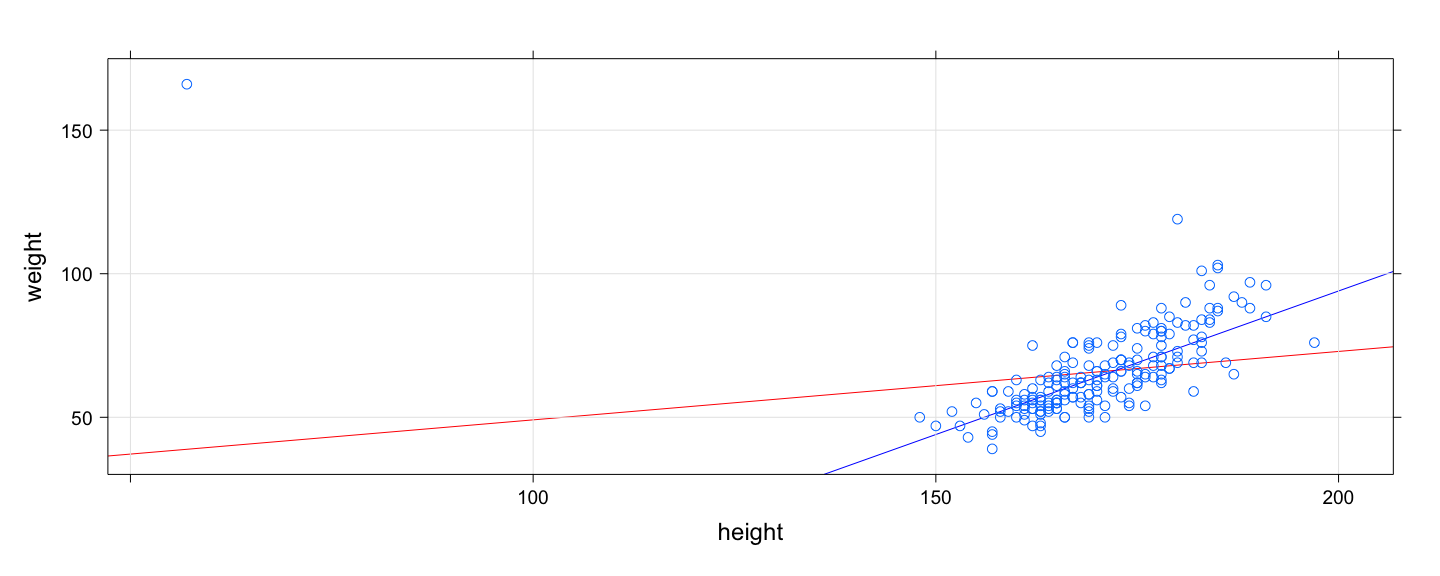
       })
```

![plot of chunk unnamed-chunk-15](figures/roverview-2-unnamed-chunk-15-1.png)

---

# Another way to plot the data and model fits

```r
library(ggplot2)
qplot(x = height, y = weight, data = Davis) + 
	    geom_abline(intercept = coef(fm)[1], slope = coef(fm)[2], col = 2) + 
        geom_abline(intercept = opt$par[1], slope = opt$par[2], col = 3)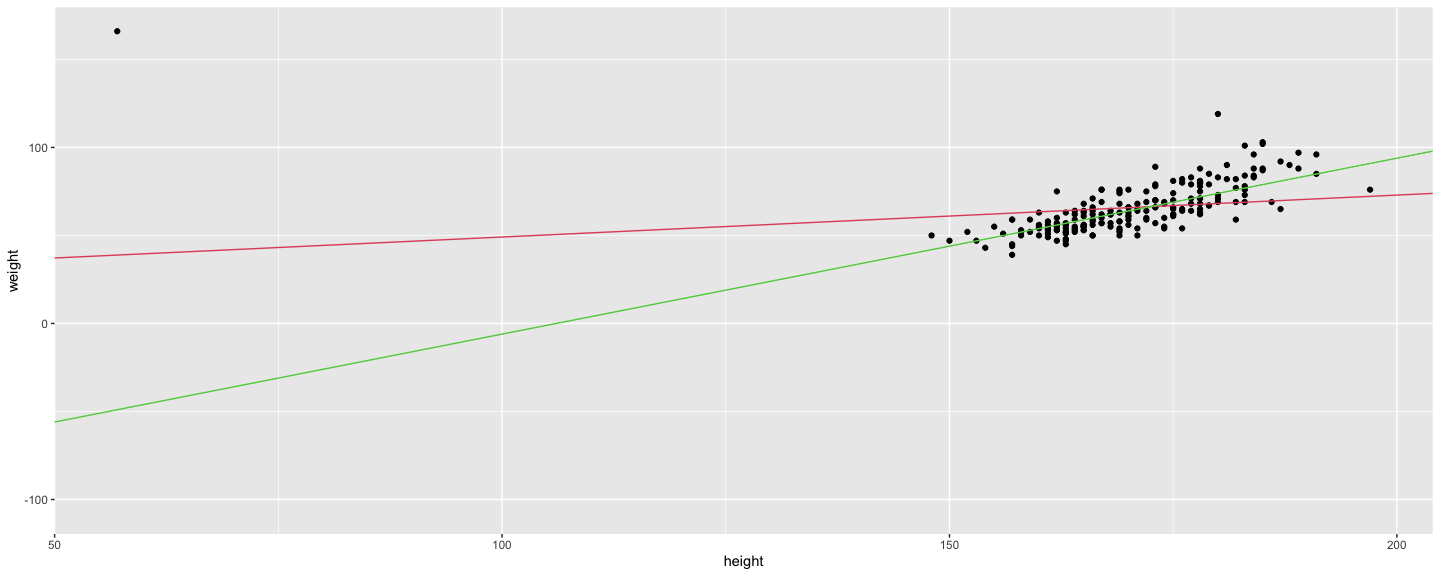
```

![plot of chunk unnamed-chunk-16](figures/roverview-2-unnamed-chunk-16-1.png)

---

# With an easy way to make the plot interactive

```r
library(plotly)
ggplotly(qplot(x = height, y = weight, data = Davis) + 
	       geom_abline(intercept = coef(fm)[1], slope = coef(fm)[2], col = 2) + 
           geom_abline(intercept = opt$par[1], slope = opt$par[2], col = 3))
```

---

# Test for slope

* Natural follow up question: Is slope non-zero?

* Need a test statistic

* Null distribution should not depend on $\sigma^2$

* How can we find one?

* Suppose we somehow obtain a test statistic

* How can we obtain the corresponding $p$-value?

---

# Simulation

* R can be used to simulate random events

* Example: how likely is a common birthday in a group of 20 people?

```r
N <- 28
days <- sample(365, N, rep = TRUE)
days
```

```
 [1] 112  66 311 109 161  47 183 276 210 255  90 146 207 229 298  75 294 358 340 253  21 137 219 256
[25]  83 278 179 172
```

```r
length(unique(days))
```

```
[1] 28
```

---

# Law of Large Numbers

* With enough replications, sample proportion should converge to probability (consistency)

---

```r
haveCommon <- function()
{
    days = sample(365, N, rep = TRUE)
    length(unique(days)) < N
}
haveCommon()
```

```
[1] FALSE
```

```r
haveCommon()
```

```
[1] TRUE
```

```r
haveCommon()
```

```
[1] FALSE
```

```r
haveCommon()
```

```
[1] FALSE
```

---

* Do this sytematically:

```r
replicate(100, haveCommon())
```

```
  [1] FALSE FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE FALSE  TRUE FALSE FALSE  TRUE FALSE
 [16]  TRUE  TRUE FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE FALSE  TRUE  TRUE
 [31] FALSE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE  TRUE  TRUE FALSE  TRUE  TRUE
 [46]  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE FALSE  TRUE  TRUE
 [61]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE
 [76]  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
 [91]  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
```

---

```r
plot(cumsum(replicate(1000, haveCommon())) / 1:1000, type = "l", ylim = c(0.5, 1))
lines(cumsum(replicate(1000, haveCommon())) / 1:1000, col = "red")
lines(cumsum(replicate(1000, haveCommon())) / 1:1000, col = "blue")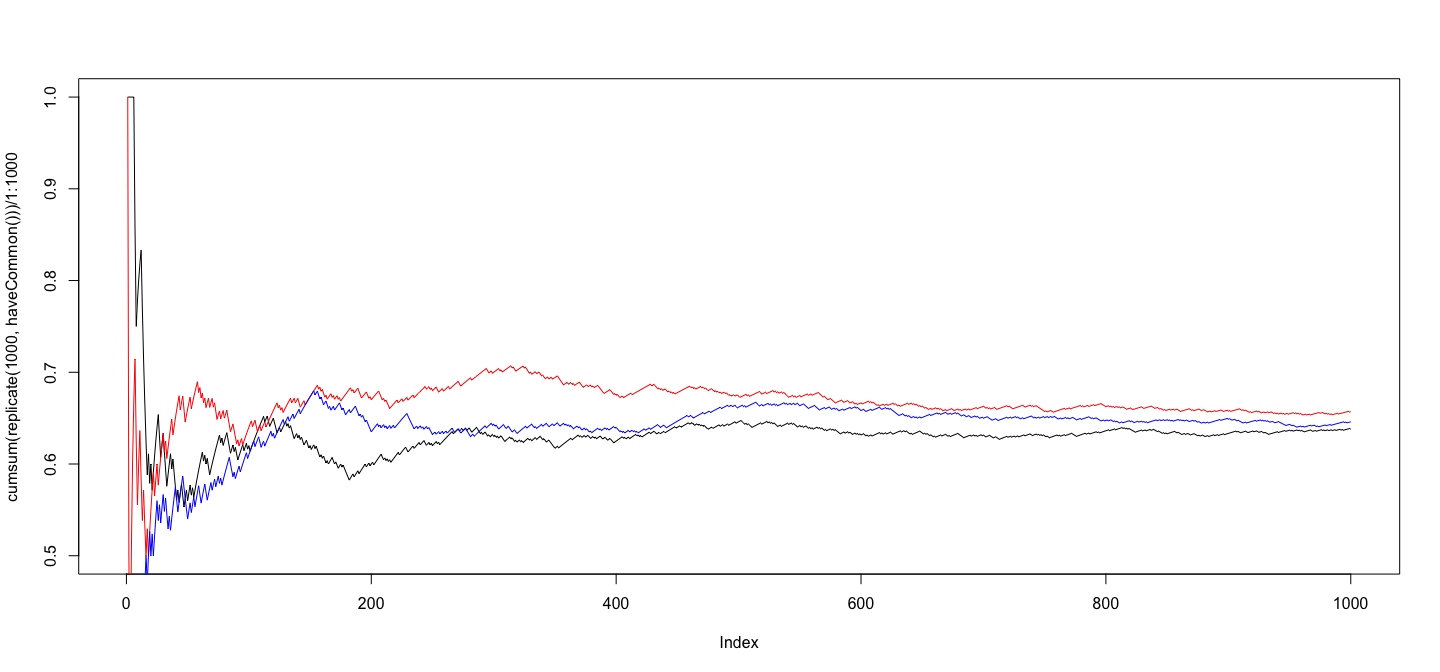
```

![plot of chunk unnamed-chunk-22](figures/roverview-2-unnamed-chunk-22-1.png)

---

# R gives access to an extensive toolset

* Most standard data analysis methods are already implemented

* Can be extended by writing add-on packages

* Thousands of add-on packages are available

- The last few plots are all created using add-on packages

---

# Drawbacks

* Learning R needs some effort

* Not point-and-click software

* Command-line interface

---

# Good practices

* Use a good interface (R Studio is the most popular one)

* Save your code in a script file (makes it easier to reproduce later)

* Use "literate programming" approaches (notebooks, R Markdown, etc.)

* Demo using R using [R script](https://github.com/deepayan/deepayan.github.io/blob/master/courses/introductory-computer-programming/slides/03-roverview-2.R) and an [R Markdown](https://github.com/deepayan/deepayan.github.io/blob/master/courses/introductory-computer-programming/slides/03-roverview-2.rmd) file