Non-Standard Evaluation

# Non-Standard Evaluation - 1

## Introductory Computer Programming

### Deepayan Sarkar

---

# R is not C

* R syntax is superficially similar to C

* This makes it easy to start using R if you are already familiar with C

* However, the internals of how R works is very different (even apart from vectorized arithmetic)

* We will try to go over some of these differences and highlight R "good practices"

---

<!--

# Some important features of R

* Lazy evaluation

* Working with "expressions"

* Non-standard evaluation

* Functions can be arguments of other functions

* The `*apply` family of functions

* Working with matrices

* Basic linear models

-->

# Topics we will cover today

* Lazy evaluation

* Working with "expressions"

* Non-standard evaluation

<!--

# Example: the probability problem discussed in class

```r
probdiv1 <- function(n, nrep)
{
    count <- 0
    for (i in seq_len(nrep)) { # or i in 1:nrep
        s <- sort(sample(n, 2))
        if (s[2] %% s[1] == 0) count <- count + 1
    }
    return (count / nrep)
}
probdiv3 <- function(n)
{
    a <- seq_len(floor(n/2))
    counts <- floor(n / a) - 1
    return (sum(counts) / choose(n, 2))
}
```

-->

---

# Lazy evaluation

---

* Arguments passed as function arguments are _not_ evaluated until they are used

* This might seem like a very minor difference

* This feature allows for some interesting behaviour in R

---

```r
rchoose1 <- function(u, a, b)
{
    if (u < 0.5) a else b
}
set.seed(20210101) # makes subsequent "random" numbers reproducible
rchoose1(runif(1), sqrt(2), sqrt(-2))
```

```
[1] 1.414214
```

```r
rchoose1(0.25, sqrt(2), sqrt(-2))
```

```
[1] 1.414214
```

```r
rchoose1(0.75, sqrt(2), sqrt(-2))
```

```
Warning in sqrt(-2): NaNs produced
```

```
[1] NaN
```

---

* Compare with a similar function written in C++

```cpp
#include <Rcpp.h>

double cchoose1(double u, double a, double b)
{
    if (u < 0.5) return a;
	else return b;
}

double wsqrt(double x)
{
	if (x < 0) Rcpp::warning("negative input: NaN produced");
	return sqrt(x);
}

// [[Rcpp::export]]
double cchooseSqrt(double u, double a, double b)
{
	return cchoose1(u, wsqrt(a), wsqrt(b));
}
```

---

```r
set.seed(20210101)
cchooseSqrt(runif(1), 2, -2)
```

```
Warning in cchooseSqrt(runif(1), 2, -2): negative input: NaN produced
```

```
[1] 1.414214
```

```r
cchooseSqrt(0.25, 2, -2)
```

```
Warning in cchooseSqrt(0.25, 2, -2): negative input: NaN produced
```

```
[1] 1.414214
```

```r
cchooseSqrt(0.75, 2, -2)
```

```
Warning in cchooseSqrt(0.75, 2, -2): negative input: NaN produced
```

```
[1] NaN
```

---

# Quoted expressions and evaluation

---

* Remember that R works by evaluating "expressions" typed at the prompt

* Consider the following expression:

```r
a < b
```

```
Error in eval(expr, envir, enclos): object 'a' not found
```

* This fails because the variables `a` and `b` used in the expression are not defined

---

* It is possible to store an expression without _evaluating_ it in R

* This can be done is several ways; for example

```r
e1 <- quote(a < b)
e2 <- expression(a < b)
```

---

* We can explore the nature of these objects in the usual ways

```r
class(e1)
```

```
[1] "call"
```

```r
length(e1)
```

```
[1] 3
```

```r
str(e1)
```

```
 language a < b
```

---

* `expression()` essentially allows a multiple quoted expressions to be stored (as a vector)

```r
class(e2)
```

```
[1] "expression"
```

```r
length(e2)
```

```
[1] 1
```

```r
length(e2[[1]])
```

```
[1] 3
```

```r
str(e2[[1]])
```

```
 language a < b
```

---

* Why is this useful?

* Among other things, expressions can be evaluated using the `eval()` function

```r
x <- 10
eval(quote(sqrt(x)))
```

```
[1] 3.162278
```

---

* Trying to evaluate `e1` again gives the same error because `a` and `b` are not defined

```r
e1
```

```
a < b
```

```r
eval(e1)
```

```
Error in eval(e1): object 'a' not found
```

* However, `eval()` has an optional `envir` argument that can be used to provide missing variables

```r
d <- list(a = rnorm(10), b = rexp(10))
eval(e1, envir = d)
```

```
 [1]  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE
```

---

# Lazy evaluation and `substitute()`

---

* Lazy evaluation allows a special trick

* An R function can quote an argument without evaluating it

* This is done using the function `substitute()`

```r
getExpression <- function(x)
{
    return(substitute(x))
}
getExpression(sqrt(10))
```

```
sqrt(10)
```

```r
getExpression(a + b)
```

```
a + b
```

---

* This can be often quite useful

* For example, the following function attaches an attribute storing
  the call to the result of any evaluation

```r
withCall <- function(e)
{
    ans <- eval(e)
    attr(ans, "call") <- substitute(e)
    return(ans)
}
withCall(sqrt(10))
```

```
[1] 3.162278
attr(,"call")
sqrt(10)
```

```r
withCall(rbind(rnorm(5), rexp(5)))
```

```
          [,1]      [,2]       [,3]      [,4]      [,5]
[1,] -1.412479 0.3771837 -0.5326313 1.0322354 0.6610746
[2,]  2.578773 0.8482034  0.2733861 0.3399451 3.1885165
attr(,"call")
rbind(rnorm(5), rexp(5))
```

---

* This is how `plot()` can construct nice axis labels

```r
x <- seq(-10, 10, length.out = 201)
plot(x = x, y = x * sin(x), type = "l")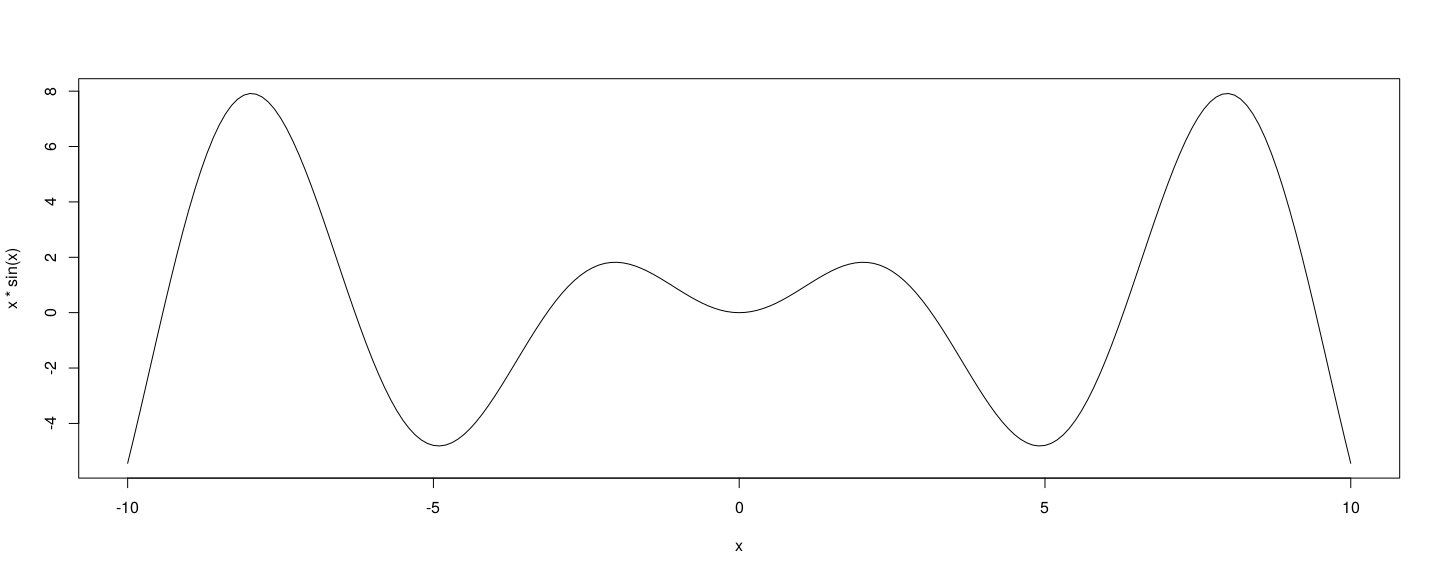 
```

![plot of chunk unnamed-chunk-14](figures/nseval-1-unnamed-chunk-14-1.png)

---

* And how `curve()` determines what function to plot

```r
curve(x * sin(x), from = -10, to = 10)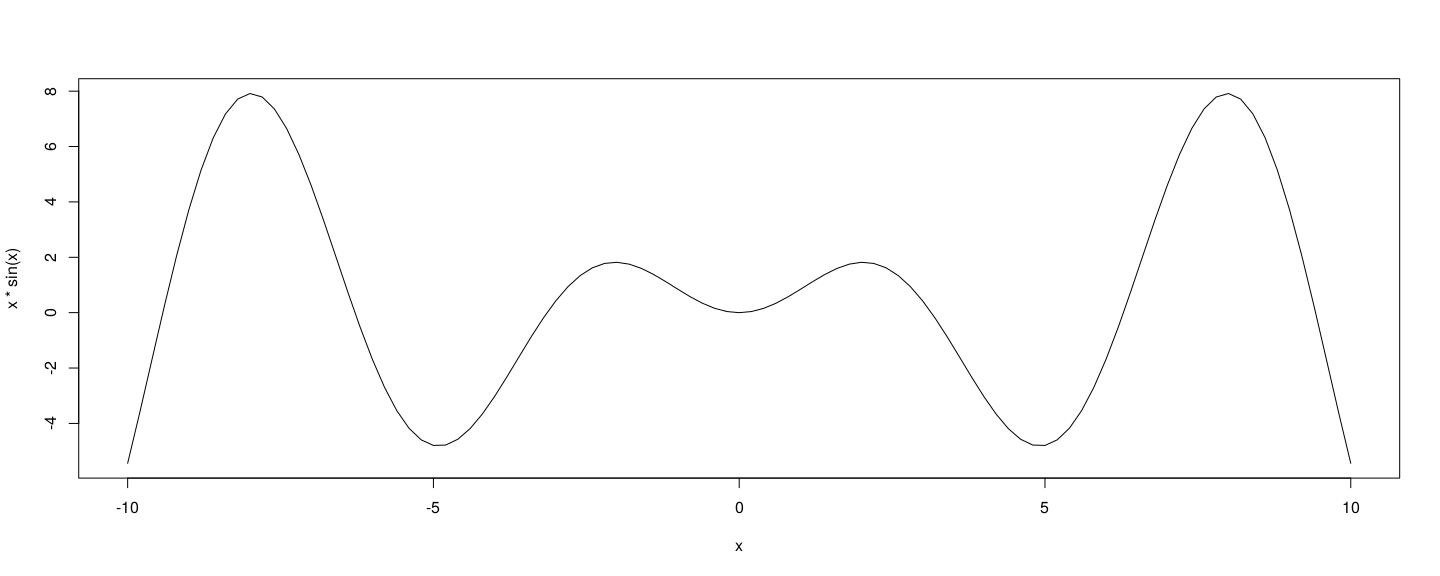
```

![plot of chunk unnamed-chunk-15](figures/nseval-1-unnamed-chunk-15-1.png)

---

# Questions?

<!--

```r
e1[[1]]
```

```
`<`
```

```r
e1[[2]]
```

```
a
```

```r
e1[[3]]
```

```
b
```

```r
e1[[1]] <- quote(rbind)
e1
```

```
rbind(a, b)
```

```r
eval(e1, envir = d)
```

```
       [,1]       [,2]       [,3]      [,4]         [,5]      [,6]      [,7]       [,8]     [,9]
a 0.3556914 -0.4913036 -0.6801197 -1.068554 -0.440427551 1.2370412 -1.215399 -0.2744189 1.556999
b 0.8630517  1.1707217  1.0798985  1.101444  0.004995799 0.5066633  1.264804  0.7895531 2.279978
      [,10]
a -1.243647
b  2.419367
```

-->