Introduction

The rip.recover package provides tools for image recovery or reconstruction. In an abstract sense, this is the problem of estimating an (unobserved) latent image given a degraded version that has been observed. In practice, only certain specfic types of image degradation are handled by this package, and an even more specific set of solutions (estimators) are implemented.

Generally speaking, the types of degradation that are considered are (a) blurring or convolution by a blur kernel or point spread function (PSF), (b) downscaling, and (c) noise.

The classical solution to the non-blind deconvolution problem, which is to reconstruct a blurred image (with added noise) when the blur kernel is known, is the Richardson-Lucy algorithm. This is implemented through the rip.deconvlucy() function.

The main contribution of the package is to provide an alternative Bayesian approach that uses a prior on image gradients to implement a unified solution to both deconvolution and upscaling (super-resolution). The prior also allows for image gradients to be correlated. In addition to the usual conjugate-gradient approach, the package also implements a direct solution using sparse matrix computations (via the Matrix package). The latter approach allows missing values in the input image, and these are imputed to provide a form of inpainting. See help(rip.deconv) for details.

The blur kernel is usually unknown in practice. This package also provides a fast and simple procedure to estimate a blur kernel from a blurred input image, assuming the same prior for image gradients. This is of limited use because it assumes symmetry of the blur kernel; this gives reasonable results for blurring due to slight lack of focus, but is unable to handle blurring due to camera shake. The procedure is implemented as the symmetric.blur() function.

Example: estimation of blur kernel

For illustration, we will use an example image from the opencv package README.

suppressMessages(library(rip.recover))
if (!file.exists("unconf18.jpg"))
    download.file("https://jeroen.github.io/images/unconf18.jpg", dest = "unconf18.jpg")
y <- rip.import("unconf18.jpg", type = "original") / 255
y

[3264 x 4896] image with 3 channel(s)

This is a fairly large image, and we will work with a cropped subimage.

a <- as.array(y)
o <- round(0.5 * dim(a)[1:2])
z <- as.rip(a[-350:350 + o[1], -700:700 + o[2], , drop = FALSE])
z

[701 x 1401] image with 3 channel(s)

image(255 * z, rescale = FALSE)

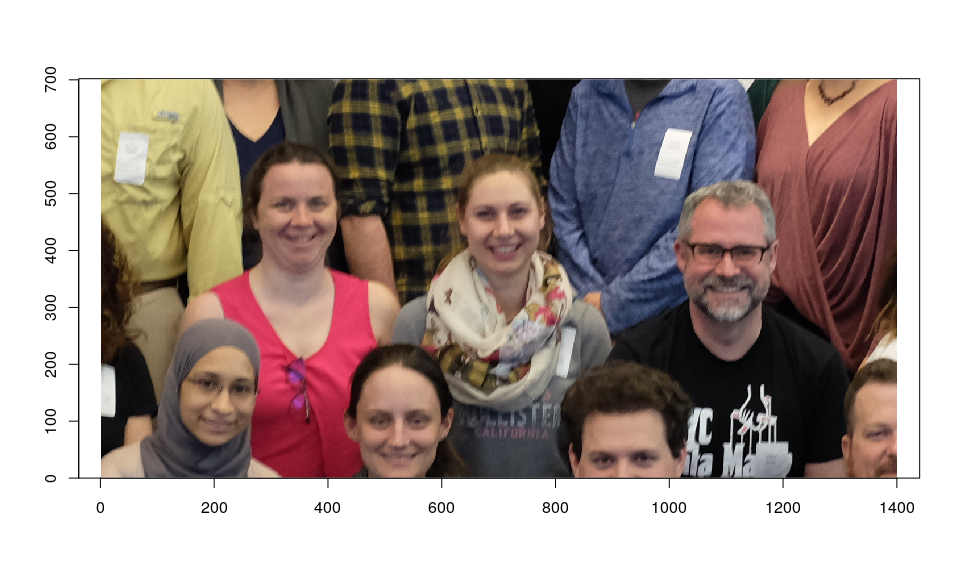
In principle, one should perform gamma correction on the input image first to make the pixel values proportional to scene brightness. This usually does not make much difference, but we will do it (approximately) anyway.

GAMMA <- 2.2
z[] <- z^(1/GAMMA)

The image above is blurred, but only slightly, and the symmetric.blur() function may be able to estimate the blur kernel reasonably well.

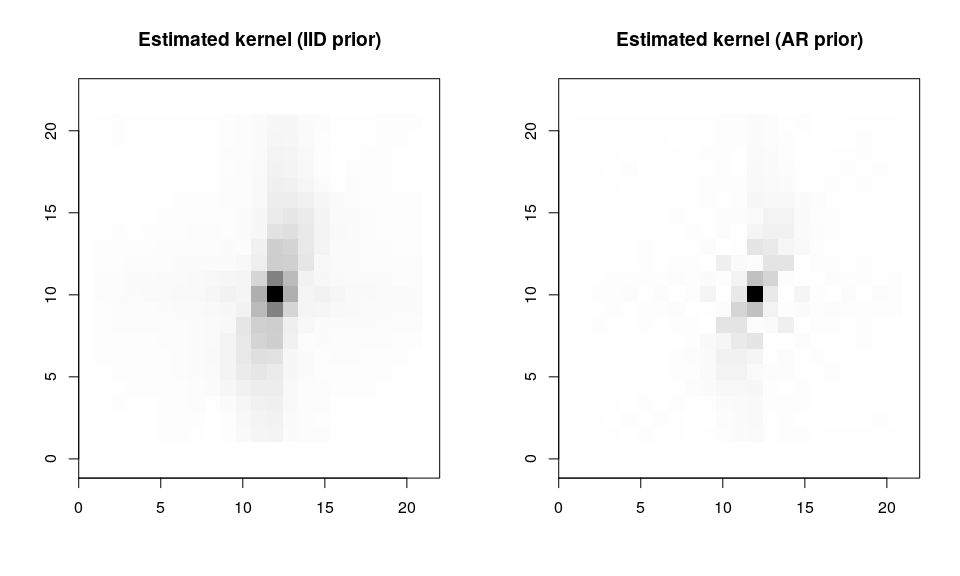
khat.iid <- symmetric.blur(z, kdim = c(10, 10), g.method = "none", trim = FALSE)
khat.ar <- symmetric.blur(z, kdim = c(10, 10), g.method = "autoreg", trim = FALSE)
par(mfrow = c(1, 2))
image(-khat.iid, main = "Estimated kernel (IID prior)")
image(-khat.ar, main = "Estimated kernel (AR prior)")

Example: Richardson-Lucy deconvolution

To deblur the image using the Richardson-Lucy algorithm, we use the estimated kernel based on the AR prior, first restricting it to have a slightly smaller size.

khat <- symmetric.blur(z, kdim = c(9, 5), g.method = "autoreg", trim = FALSE)
khat

[19 x 11] image with 1 channel(s)

We can obtain the reconstructed image as follows.

x <- rip.deconvlucy(z, k = khat, niter = 50)
image(255 * x^GAMMA, rescale = FALSE)

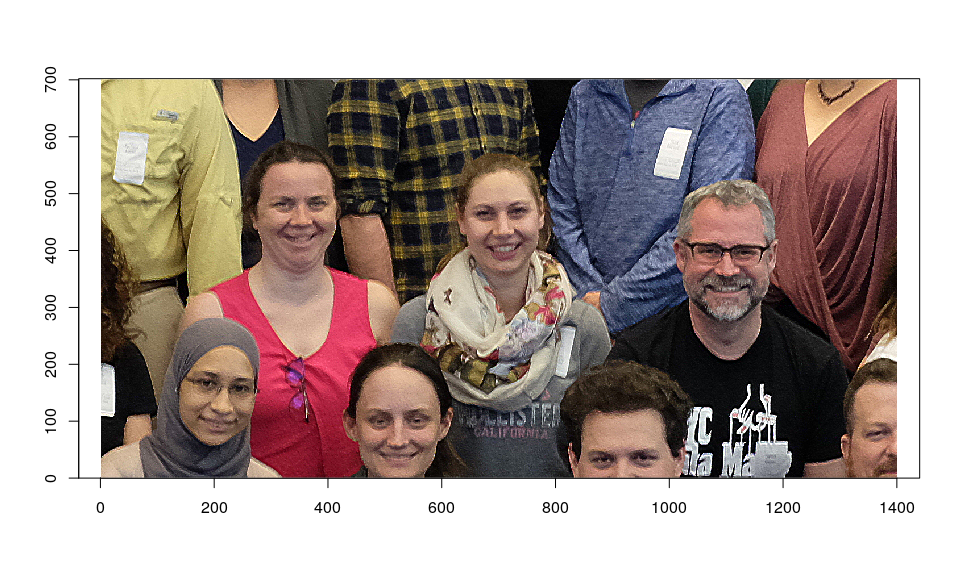
The image is now slightly sharper, although not all the blurrnig in the image has been accounted for. This is probably because at least some of the blur is due to camera shake (as opposed to lack of focus), and asymmetric, which symmetric.blur() is unable to estimate (more sophisticated methods are available for such blurs, but not yet implemented in this package).

Example: Bayesian image denoising

But another problem in the recovered image above is that it has become grainy. This is common with the Richardson-Lucy algorithm, which does not impose any regularization penalty on the estimated image. The rip.recover package allows image reconstruction using a Bayesian approach, supporting the so-called hyper-Laplacian family of priors for image gradients that also allows the gradients to be locally correlated; see help(rip.deconv) for details. This approach is much slower than the Richardson-Lucy algorithm, but a comprehensive set of examples can be found here, with the corresponding code available here.

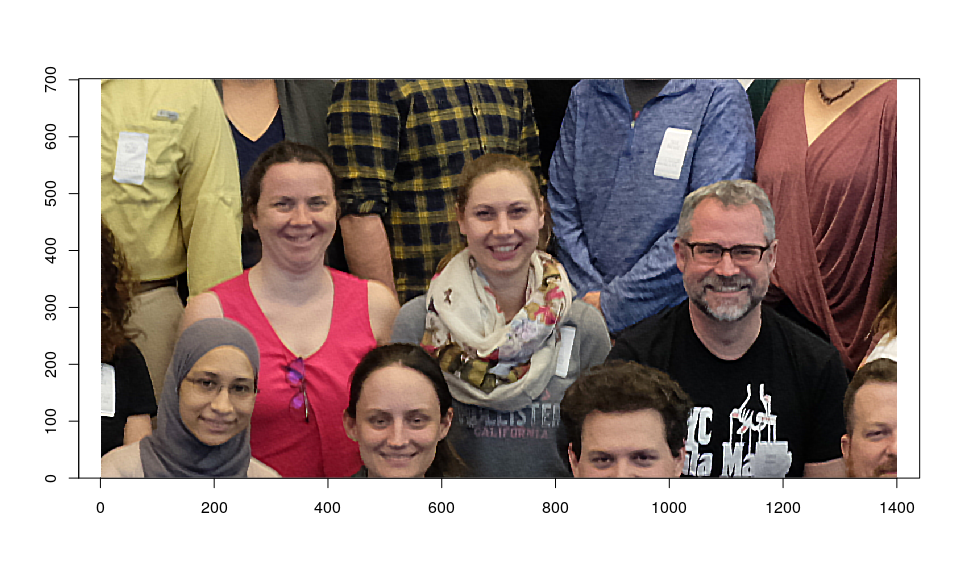
Here, instead of performing Bayesian deconvolution on the original image, we give a simpler (and faster) example where the Bayesian image reconstruction approach is used as a post-processing step to denoise the output of the Richardson-Lucy algorithm. It uses a so-called “sparse” prior ($\alpha = 0.8$), with image gradient density proportional to $e^{-\lvert x \rvert^\alpha}$, with the gradients correlated according to a 2-D auto-regressive model. In addition, a robust (Huber) loss function comparing the input and estimated images is minimized instead of squared error loss.

x2 <- rip.denoise(x, ksigma = 0, method = "direct",
                  patch = 250, overlap = 10, yerror = "huber", huber.k = 1,
                  alpha = 0.8, rho = list(along = 0.3, across = 0.6), lambda = 0.025)
image(255 * x2^GAMMA, rescale = FALSE)

The estimated images can also be exported for comparison in an external viewer.

rip.export(255 * z^GAMMA, "figure/cropped-original.jpg")
rip.export(255 * x^GAMMA, "figure/cropped-lucy.jpg")
rip.export(255 * x2^GAMMA, "figure/cropped-lucy-sparse-ar-robust.jpg")

Links:

• Original image (cropped)
• Richardon-Lucy reconstruction
• Richardon-Lucy followed by Bayesian reconstruction

The project page on Github can be used for bug reports and patches.